All posts in Book Summary

Daniel Dennett, who recently passed away, is an inspiration for people like me who love grand ideas that connect many different fields at a deep level (and be rigorous about that; well as rigorous as grand theories can be). His thinking is difficult to categorize: part philosopher, part scientist, he had many good ideas on topics ranging from evolution to consciousness to God.

The book From Bacteria To Bach And Back had been lying on my shelf for many years and I recently picked it up because I’ve been thinking a lot about evolutionary constraints on brain and consciousness. ...  Read the entire post →

I just finished this tremendously readable and provocative book: Escape from Shadow Physics.

The book is about foundations of quantum mechanics. To be precise, it’s about why we should not give up on trying to find a deeper theory of quantum mechanics.

The usual story in QM is that the theory is complete and the probabilistic nature of our measurements is just the way nature is. Einstein famously rebelled against this, and didn’t accept it even until his death.

Believe it or not, this attitude of his — “God does not play dice” — is in minority today. Most of the modern physicists believe that QM is complete, and that at the micro level reality is simply probabilistic when you make observations. In other words, there’s no deeper explanation to why we get statistical outcomes in QM experiments. ...  Read the entire post →

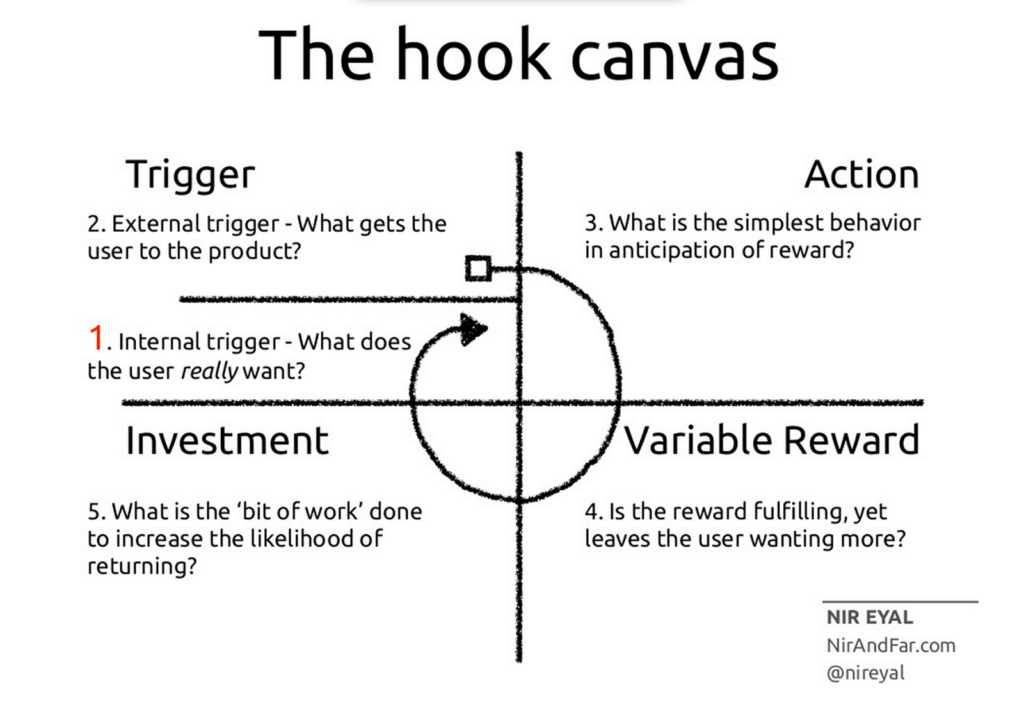
I recently finished a very short book with an intriguing title: Why Greatness Cannot be Planned.

It’s an unconventional self-help book disguised as a computer science research exposition (that’s why the publisher is Springer). I strongly recommend reading it. Here is a taste of the book’s main ideas.

Objectives only work when your goal is one hop away from where you are

Setting a goal makes sense when you know how to achieve them. Let’s say you’re a published author working on your next book and you already have an agreement with a publisher. In this case, setting an objective for yourself that you should finish the first draft by a specific date makes sense because everything is in place for you to achieve it. ...  Read the entire post →

I’ve started reading The Capitalist Manifesto, a book full of data on how free markets generate prosperity.

The author is nuanced and uses data and logic to show how we should be rooting for capitalism (instead of bringing it down).

Income and wealth inequality created as a function of entrepreneurship is not a bad thing per se. Risk-takers and innovators derive a higher income when they create much more value elsewhere.

Nobody hands over a million dollars to someone else for free. Profit earned by someone in free markets is typically a surplus made available to them because they expanded the pie for everyone. (And not because they stole it from someone else. Capitalism is NOT a zero-sum game.) ...  Read the entire post →

Finished (well, skimmed) the book “Decoding the Why: How Behavioral Science is Driving the Next Generation of Product Design”. It’s a decent introductory book if you have not delved into behavioral science before, but if you have, most of the ideas in the book won’t come across as surprising or new.

Nevertheless, made some quick notes.

1/ Imagining the future as concretely as possible helps us align our actions towards the future self (otherwise, the future self remains an abstract, theoretical concept).

So, whenever you can, help people imagine the benefit of making a change in their life via your product. ...  Read the entire post →